Find the Quadratic Polynomial Which Best Fits the Data Points

Curve fitting can involve either interpolation where an exact fit to the data is required or smoothing in which a smooth function is constructed that approximately fits the data. Its up to you to decide the age at which its most meaningful to interpret the intercept.

Polynomial Curve Fitting Matlab Simulink Example

24 plot points screenplay.

. The exact value you center on doesnt matter as long its meaningful holds the same meaning across samples and within the range of data. As a result multiple fits using the same data and model might. Curve fitting is the process of constructing a curve or mathematical function that has the best fit to a series of data points possibly subject to constraints.

It is also slow in fitting the data due to the calculation of pair-wise distances among data points. The most common type of linear regression is a least-squares fit which can fit both lines and polynomials among other linear models. For rational and Weibull models and all custom nonlinear models the toolbox selects default initial values for coefficients uniformly at random from the interval 01.

It is easy to use and to tune easily copes with large gaps in the data empty areas where function values are unknown. Numpy polyfit is a method available in python that fits the data within a polynomial function. The quadratic fits the standard quadratic function to the actual data.

And the actual is the unconstrained age-experience curve. You may find that choosing the lowest value or the highest value of age is the best option. These results are shown in Table 6-1 separately for college and high school graduates.

The convex hull would be represented by a tight rubber band that surrounds all the nails. This yields three different experience curves. A line plot is a type of plot which displays information as a series of data points called markers connected by straight line segments.

However it is clear that despite the left model having a higher R². In this article different aspects such as syntax working and examples of polyfit function are explained in detail. Use this method when your data is highly nonlinear and limited and you want your model to fit right through your data ie you trust your simulation results.

Here it least squares the function polynomial fit. He points to two potential factors in the delay. The most common type of linear regression is a least-squares fit which can fit both lines and polynomials among other linear models.

Use the model you found in part b to find the distance a baseball travels when it is hit at an angle of. A data model explicitly describes a relationship between predictor and response variables. Both models above have predicted lines that give a strong fit in that they have high R² values and also capture the small deviation of the actual data points from the fitted line.

A related topic is regression analysis which. Linear regression fits a data model that is linear in the model coefficients. To fit curve to experimental data containing noise then the best choice is to use penalized regression spline.

Linear regression fits a data model that is linear in the model coefficients. Rather than finding cubic polynomials between subsequent pairs of data points Lagrange polynomial interpolation finds a single polynomial that goes through all the data pointsb Fit the data with linear and spline interpolations and use each interpo-lation to estimate the height in day 40If you determine you have an Intel GPU on your machine make. Left a quadratic model predicted linearly Right a linear model predicted linearly.

We are given n points in the plane and we wish to find the convex hull of these points. Intuitively we can think of each point as being represented by a nail sticking out from a board. However this method automatically fits through all data points.

That is transforming the x values is appropriate when non-linearity is the only problem the independence normality and equal variance conditions are met. Smoothing degree can vary in very wide range - from almost 100 damping of all nonlinearities result is a straight line to almost 100 absence of. The convex hull is the smallest convex polygon containing the points.

Data visualization is used to explore a given dataset and perform data analytics and build predictive models. This might be the first thing that you try if you find a lack of linear trend in your data. Use the regression feature of the graphing calculator to find a linear or quadratic model that best fits the data12019075400 c.

In this section we learn how to build and use a simple linear regression model by transforming the predictor x values. A data model explicitly describes a relationship between predictor and response variables. The quartic fit is the result of Lemieuxs equation.

If no start points the default value of an empty vector are passed to the fit function starting points for some library models are determined heuristically. Matplotlib was created by John Hunter an American neurobiologist and was originally developed as an. That is a polynomial pX of deg degree is fit to the coordinate points X Y.

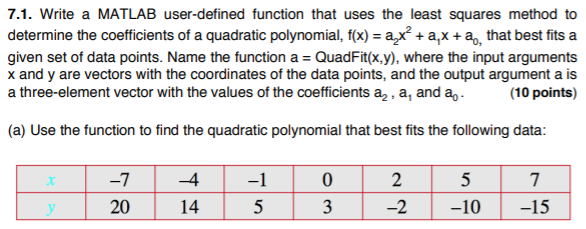
Solved 7 1 Write A Matlab User Defined Function That Uses Chegg Com

Identifying And Writing Quadratic Functions From Data Youtube

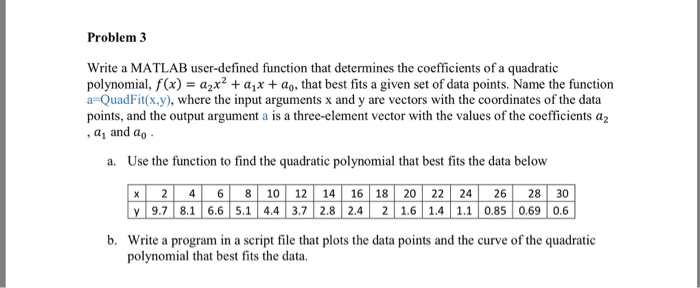
Solved Write A Matlab User Defined Function That Determines Chegg Com